그냥 게임개발자
인접리스트 본문
우리는 저번 포스팅에 인접행렬을 배웠습니다.
2차원 배열이죠
그렇다면 인접리스트는 무엇일까요?
연결리스트 여러개 묶은 것이 인접리스트입니다.

이러한 그래프가 있습니다.
그렇다면 이것을 인접리스트로 어떻게 표현할까요?
각 인덱스의 정점을 넣는겁니다.
list0[1, 4]
list1[0, 2, 3, 4]
list2[1, 3]
list3[1, 2, 4]
list4[0, 1, 3]이런식으로 말이죠.
그렇다면 진짜 코드를 짜보죠.
#include <iostream>
#include <vector>
using namespace std;
const int VERTEX = 5;
vector<int> adj[VERTEX];
int main()
{
adj[0].push_back(1);
adj[0].push_back(4);
adj[1].push_back(0);
adj[1].push_back(2);
adj[1].push_back(3);
adj[1].push_back(4);
adj[2].push_back(1);
adj[2].push_back(3);
adj[3].push_back(1);
adj[3].push_back(2);
adj[3].push_back(4);
adj[4].push_back(0);
adj[4].push_back(1);
adj[4].push_back(3);
}
이게 인접리스트입니다.
간단하죠?
그냥 인접배열은 2차원 배열로 0을 포함한 배열들인데
인접리스트는 정말 정점과 정점끼리 연결된 애들끼리만 모아놓은 리스트입니다.
그렇다면 이것을 확인해봅시다.
#include <iostream>
#include <vector>
using namespace std;
const int VERTEX = 5;
vector<int> adj[VERTEX];
int main()
{
adj[0].push_back(1);
adj[0].push_back(4);
adj[1].push_back(0);
adj[1].push_back(2);
adj[1].push_back(3);
adj[1].push_back(4);
adj[2].push_back(1);
adj[2].push_back(3);
adj[3].push_back(1);
adj[3].push_back(2);
adj[3].push_back(4);
adj[4].push_back(0);
adj[4].push_back(1);
adj[4].push_back(3);
for (int i = 0; i < VERTEX; ++i)
{
cout << "list" << i << " ";
for (int there : adj[i])
{
cout << there << " ";
}
cout << '\n';
}
}
이런식으로 확인이 가능합니다.
결과물을 확인해보죠.
list0[1, 4]
list1[0, 2, 3, 4]
list2[1, 3]
list3[1, 2, 4]
list4[0, 1, 3]
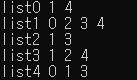
어때요 결과물이 같죠?
근데 왜 인접 리스트인데 list를 사용하지 않고 vector를 사용했을까요.
물론 list도 가능하지만 이것은 시간 복잡도의 차이를 보면 알 수 있습니다.
| n번째 삽입, 삭제 | 마지막 요소에 삽입, 삭제 | 특정 요소 탐색 | n번째 요소 참조 | |
| list | O(1) | O(1) | O(n) | O(n) |
| vector | O(n) | O(1) | O(n) | O(1) |
여기서 보면 삽입 삭제는 list가 더 빠른데 참조는 vector가 더 빠릅니다.
list는 선형구조이며 순차접근입니다.
vector는 비선형구조이며 랜덤접근입니다.
그래서 사실 아무거나 사용해도 되긴한데 참조가 더 빨라서 그냥 저는 vector를 주로 사용합니다.
그러면 인접리스트를 통한 방문을 체크하는 재귀함수를 사용해보죠.
#include <iostream>
#include <vector>
using namespace std;
const int V = 10;
vector<int> adj[V];
int visited[V];
void solve(int _idx)
{
// 방문
visited[_idx] = 1;
for (int there : adj[_idx])
{
if (visited[there])
continue;
solve(there);
}
}
int main()
{
adj[0].push_back(1);
adj[0].push_back(4);
adj[1].push_back(0);
adj[1].push_back(2);
adj[1].push_back(3);
adj[1].push_back(4);
adj[2].push_back(1);
adj[2].push_back(3);
adj[3].push_back(1);
adj[3].push_back(2);
adj[3].push_back(4);
adj[4].push_back(0);
adj[4].push_back(1);
adj[4].push_back(3);
for (int i = 0; i < V; ++i)
{
// adj 벡터의 사이즈가 0이 아니라면
// 어떠한 값이 있다는 것 즉 연결된 정점들이 들어있다라는 뜻
if (adj[i].size() && visited[i] == false)
solve(i);
}
return 0;
}
끄으으읕
'내 개인적인 공부 > 알고리즘' 카테고리의 다른 글
| 맵과 방향 벡터 (0) | 2024.04.22 |
|---|---|
| 인접행렬과 인접리스트의 차이 (0) | 2024.04.22 |
| 인접행렬(2) (0) | 2024.04.22 |
| 인접 행렬(1) (0) | 2024.04.21 |
| 이진 트리와 이진 탐색 트리 (1) | 2024.04.21 |




