그냥 게임개발자
등비수열 본문
등비수열이란?
한 항과 다음 항의 비율이 같은 수열을 등비수열이라고 합니다.
예를 들어
4, 12, 36, 108 ...이라는 숫자가 있다고 보았을 때
12라는 숫자는 4로 나누었을 때 3이라는 숫자가 나옵니다.
36은 12라는 숫자로 나누었을 때 3이라는 숫자가 나오구요.
그러면 다시 4에서 3을 곱하면 12가나오죠 12에서 3을 곱하면 36이나오죠.
이렇 듯 공통비율을 가진 것들을 등비수열이라고 합니다.
모두 3배씩 증가하기 때문에 3을 공비라 하며, 첫번째 항을 초항이라고 합니다.
그렇다면 공비가 3이고 초항이 4인 등비수열이라고 표현할 수 있습니다.
등비수열에는 2개의 공식이 있습니다.

우리가 위에서 예를 들은 것을 넣어보죠.
만약 더할 숫자가 108까지 4, 12, 36, 108 이렇게 4개라고 하면
a = 4
r = 3
n = 4개를 대입했을 때,
4(3^4 - 1) / 3 - 1입니다.
4(80) / 2가 되며
320 / 2 = 160이 됩니다.
그러면 맞는지 확인해봅시다.
4 + 12 + 36 + 108은?

정확하네요.
수학자들은 똑똑합니다.
증명할 필요가 없어지네요

그렇다면 두번째 공식도 확인해보죠.

이거는 n이 무한대로 되었을 때와 r이 -1보다는 크고 1을 넘지 않는 숫자일 때 사용하는 공식입니다.
확인해보죠.
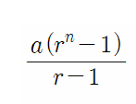
아까 첫번째 공식을 이용해서
a = 4
r = 3
n = ∞
라고 치면
a(r^ ∞ - 1) / r - 1인데
r^ ∞는 무엇일까요?
뭐 예를 들어 r이 아까 -1과 1을 넘지 않는다면 자연수로 치면 0일 텐데
뭐 1/2라고 치죠
그러면



이 순서대로 되겠죠? 그러면 거의 0에 가까워지죠?
거의 0에수렴합니다!
그러면 r^ ∞는 거의 0이라고 해도 무방하죠.
그럼 다시 식을 봅시다.
a(0-1) / r -1이 됩니다.
그럼 최종적으로 a / r - 1이되죠
우하하
맞네요



아 뭐 일단 증명은 되었잖아요?
그런데 우리는 첫번째 공식을 자주 사용할 겁니다.
코드로 확인해보죠
뭐 우리가 아까 예를 들었던
초항이 4 공비가 3 숫자의 개수가 4개일때를 코드로 작성해보죠.
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int a = 4, r = 3, n = 4;
vector<int> vec;
cout << a *((int)pow(r, n) - 1) / (r - 1);
cout << '\n';
for (int i = 0; i < n; ++i)
{
vec.push_back(a);
a *= r;
}
for (int i : vec)
cout << i << ' ';
}
오 잘 나왔네요.
그럼 끄으틍
'내 개인적인 공부 > 수학' 카테고리의 다른 글
| 등차수열 (0) | 2024.04.21 |
|---|---|
| 에라토스테네스의 체 (0) | 2024.04.21 |
| 모듈러 연산 (0) | 2024.04.21 |
| 조합 (코드 포함) (1) | 2024.04.21 |
| 순열 (0) | 2024.04.21 |



