그냥 게임개발자
등차수열 본문
등차수열이란 1부터 n까지의 합을 구하는 공식이다.
시그마라 하죠.
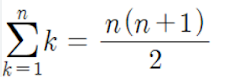
이 등차수열을 예를들어 n = 5라고 치게 되면
5(5 + 1) / 2 = 30 / 2 = 15라는 값이 나온다.
1 + 2 + 3 + 4 + 5 = 15가 나오죠.
정확하죠?
그러면 코드로 확인해봅시다.
#include <iostream>
using namespace std;
int main()
{
int n = 5;
int ret = 0;
// 그냥 for문을 돌려 사용한 등차수열
for (int i = 1; i <= n; ++i)
{
// 1 + 2 + 3 + 4 + 5
ret += i;
}
cout << ret << '\n';
// for문을 사용하지 않고 사용한 등차수열
cout << n * (n + 1) / 2 << '\n';
return 0;
}
이렇게 for문을 사용하지 않고 O(1)만에 등차수열의 합을 구했습니다.
그렇다면 초항이 3이고 등차가 5, n이 5인 등차수열의 합은 어떨까요?
즉 3 + 8 + 13 + 18 + 23 = 65를 구하는 방식말입니다.
이는 등차수열의 합 공식을 통해 알 수 있습니다.

n은 더할 숫자의 개수
a는 초항
l은 마지막 합의 숫자
코드로 보시죠
#include <iostream>
using namespace std;
int main()
{
int n = 5; // 숫자의 개수
int a = 3; // 초항(시작 숫자)
int l = 23; // 마지막 숫자
cout << n * (a + l) / 2 << '\n';
return 0;
}이와 같이 65라는 숫자를 O(1)이라는 시간이 걸리는 코드를 작성할 수 있습니다.
마지막의 숫자와 시작 숫자 그리고 숫자의 개수만 알면 합을 구할 수 있습니다.
'내 개인적인 공부 > 수학' 카테고리의 다른 글
| 등비수열 (1) | 2024.04.21 |
|---|---|
| 에라토스테네스의 체 (0) | 2024.04.21 |
| 모듈러 연산 (0) | 2024.04.21 |
| 조합 (코드 포함) (1) | 2024.04.21 |
| 순열 (0) | 2024.04.21 |



