그냥 게임개발자
조합(Combination) 본문
조합이란?
순열 글을 포스팅 할 때
순서있는 건 순열
순서 상관 없이 조합
이라고 했다.
조합에는 순서가 없다.
그저 몇명을 뽑아서 갈 것인가를 쓸 때 조합을 쓴다.
순서따윈 상관없고 오로지 몇명을 '다양하게'뽑을 때 사용하는 것
공식을 먼저 보자

예를 들어 5개 중에 3개를 순서 상관없이 뽑는다면
공식에 사용되는 건 이렇다
5C3
그럼 결국 이것을 대입해보면
5! / 3!(5-3)!이다.
그럼 결국 풀어서 설명하자면
5 * 4 * 3 * 2 * 1
---------------------
3 * 2 * 1 * 2 * 1
이렇게 표현이 되겠다.
그렇다면
5 * 4 * 3 * 2 * 1
---------------------
3 * 2 * 1 * 2 * 1
뺄 것들을 빼면
5 * 4 / 2가 되어 20 / 2 = 10개가된다.
쉽지 않나?
다시 생각해보자.
[1, 2, 3, 4, 5] 중에 3개를 뽑는다면
[1, 2, 3], [1, 2, 4], [1, 2, 5], [1, 3, 4], [1, 3, 5], [1, 4, 5], [2, 3, 4], [2, 3, 5], [2, 4, 5], [3, 4, 5]
10개가 맞다.
여기서 포인트는 이거다
3개 이하를 뽑는다면 중첩 반복문
4개 이상을 뽑는다면 재귀함수가 빠르다.
일단 조합(Combination)의 코드를 보자.
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int n = 5, k = 3, a[5] = {1, 2, 3, 4, 5};
void print(vector<int> b)
{
for (int i : b)
cout << i << " ";
cout << '\n';
}
void combi(int start, vector<int> b)
{
if (b.size() == k)
{
print(b);
return;
}
for (int i = start + 1; i < n; ++i)
{
b.push_back(i);
combi(i, b);
b.pop_back();
}
return;
}
int main()
{
vector<int> b;
combi(-1, b);
return 0;
}
어우 길다 길어
이것을 도식화 해서 이해해보자.
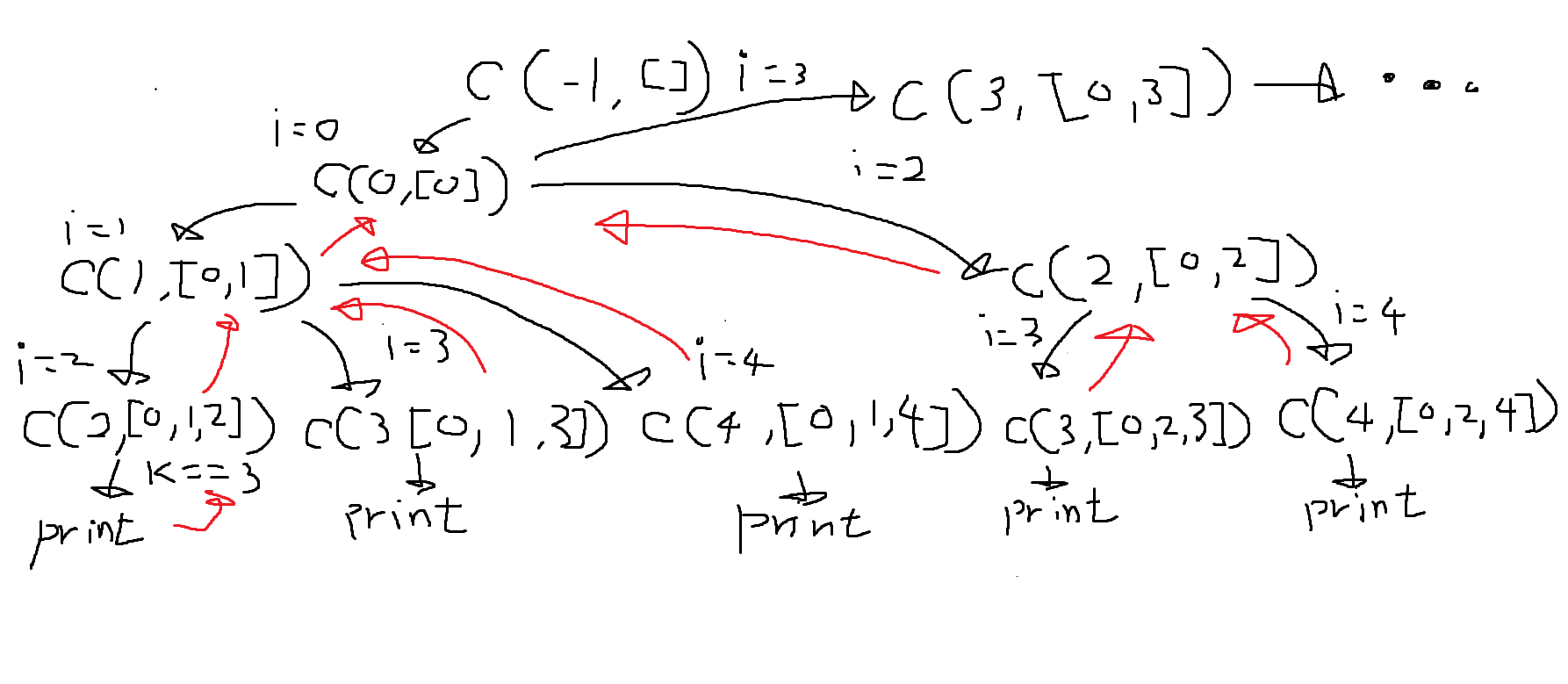
나 그림 잘 그리는 것 같아

그래서 빨간선이 return이 되는 것이고 검은선이 함수가 진행되는 선이다.
나도 도식화를 해서 그려보니 이해가 좀 간다.
그럼 이 코드를 가지고 정말 테스트를 해보자.
도식화에서는 [0, 1, 2] ~ [0, 3]까지밖에 안그렸는데
거기까지라도 맞는지 확인해보자.
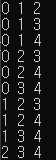
아주 정확히 잘 나왔다.
음음
맘에 들어 도식화한 보람이 있네
이정도면 코테 합격이다.

아무튼
재귀함수는 외운다실시
void combi(int start, vector<int> b)
{
if (b.size() == k)
{
// logic
return;
}
for (int i = start + 1; i < n; ++i)
{
b.push_back(i);
combi(i, b);
b.pop_back();
}
}외운다.
근데 지금 보면 b라는 vector에 i값을 넣고있다.
그런데 그러면 값은 [0, 1, 2], [0, 1, 3] ... 이런식으로 들어갈텐데
그렇다면 [2, 4, 5, 2, 3, 1] 이런 배열에는 어떻게 출력을 하게되나?
쉽다.
저 logic부분에
int a[5] = {1, 2, 3, 4, 5};
void print(vector<int> b, int[] a)
{
for (int i : b)
cout << a[i] << " ";
cout << '\n';
}
void combi(int start, vector<int> b)
{
if (b.size() == k)
{
print(b, a);
return;
}
for (int i = start + 1; i < n; ++i)
{
b.push_back(i);
combi(i, b);
b.pop_back();
}
}
ㅇㅇ 이렇게 print 해주면 된다. 인덱스에 접근해서
이제 중첩 for문이다.
중첩 for 문 조합
int n = 5;
int main()
{
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < i; ++j)
{
for (int k = 0; k < j; ++k)
{
cout << i << " : " << j << " : " << k << '\n';
}
}
}
}쉽다.
어차피 순서는 상관없다
그렇다면 이렇게 돌린 경우는 이렇게 나올 것이다.
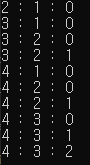
잘 나왔다. 10개
또 다른 방법도 있다.
int n = 5;
int main()
{
for (int i = 0; i < n; ++i)
for (int j = i + 1; j < n; ++j)
for (int k = j + 1; k < n; ++k)
cout << i << " : " << j << " : " << k << '\n';
}
이렇게 +1을 해서 조건을 n으로 통일 할 수 있다.
근데 조합은 순서와 상관 없이 때문에 아무거나 외우면 되는데
4개 이상은 재귀함수
3개 이하는 반복문
외워
외워
외워
외워
'내 개인적인 공부 > 알고리즘' 카테고리의 다른 글
| 암시적 형변환 (0) | 2024.04.04 |
|---|---|
| 반복문을 통한 순열 (0) | 2024.04.04 |
| 순열 - 재귀함수로 만드는 순열 (0) | 2024.04.01 |
| 순열(Permutation) (0) | 2024.03.31 |
| 재귀함수(Recursion) (0) | 2024.03.31 |




